Times Table Circles - Scaffold for memorising times tables

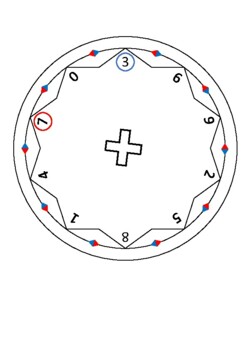
This scaffold is based on the principle that cyclic patterns form in the final digits of numbers in the times tables. When this pattern is reversed, it forms another cycle corresponding to a different times table.

For example, look at the 3 times table: (0), 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33 . The final digits 3, 6, 9, 2, 5, 8, 1, 4, 7, 0 will keep repeating on and on for ever (the same will be true for the 13, 23, 33 and so on... times tables).

If we reverse the order of the pattern for the 3 times table, we get: 7, 4, 1, 8, 5, 2, 9, 6, 3, 0 . This is actually the pattern for the 7 times table: (0), 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77 .

The same is true for the following times table pairs: 1 and 9, 2 and 8, 3 and 7, 4 and 6, with the 5 times table being easy enough to remember already.

I recomment printing, laminating and cutting this resource to make it tactile. Students can physically turn the circles around and use this as a scaffold when memorising their times tables. It is especially useful when, for example, students already know their 3 times table, but do not know their 7 times table - which is generally considered to be more difficult.

I might make different versions of this resource so that students can make and colour the times table circles themselves, and do worksheets based on the same concept.