- PDF
Description
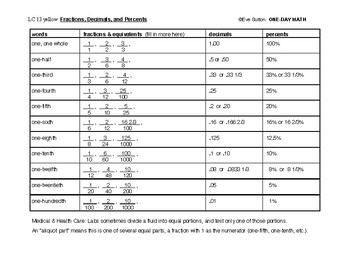
Lesson Card 13 shows the pattern of equivalent fractions and allows students to contribute more examples. Use LC 13 by itself, or with LC 14 Fractions: the Brick Wall. Most lessons will be under 30 minutes, but you can use this Lesson Card endlessly to create more lessons.
Search for these videos on YouTube.com and see how to use this Lesson Card:
"3a-3k Teach Multiplication Table; 2-min Drills to Multiply & Divide; Factors; Primes; ESL Adult [CC]" [connect factors and multiplication facts to fraction lessons]
"ONE-DAY MATH: Intro to Fractions, Decimals, Percentages--BEST Tricks for Tests or Teaching in USA" [Lesson 4f]
"How To Teach Division; convert 1/8 to decimal to percentage | ONE-DAY MATH [CC]" [Lesson 4g]
Print or Download this page for lesson ideas if you are teaching.
MATH LESSON IDEAS: Draw diagrams to show a fraction and cut the pieces or shade the pieces to show an equivalent fraction with different numerator and denominator. Play games with fractions, decimals, and percents using greater than /less than/ equal to. Use as a reference for cross-multiplication. Estimate a decimal or percent to the nearest fraction. Say a decimal number out loud to find the numerator and denominator, then write it as a fraction. Warm up for finding common denominators, expanding/reducing fractions, and converting fractions to decimals. Use as a reference when graphing linear equations. Example: Three points on a line are (1, 3) and (3, 9) and (10, 30). Find more points as ordered pairs (x, y) for this line.
ENGLISH: Text in left column helps students read and spell the names of fractions. This practice is especially good for English learners. Pronounce the plural denominators carefully (fifths, twelfths). Nortice that some are irregular (two halves, three thirds).
CAREER TECH: The text at bottom explains aliquot parts for medical and health care workers.
[See LC 14 for more lesson ideas.]
NOTE before you download and print: This download is for individual use only. See Terms of Use below.
Print this .pdf onto yellow cardstock to match Lesson Card 13 from Part 4 of ONE-DAY MATH.
Print onto white paper if you want students to color some lines to match LC 14 FRACTIONS: THE BRICK WALL
Display on screen to enlarge the image for visually impaired students.
Related items: Lesson Card 14 FRACTIONS: THE BRICK WALL and
FRACTIONS AUDIO LECTURE explaining both LC 13 and LC14: 4f-FracDecPerIntro-654.mp3
See the whole course, or just Part 4 (Fractions):
https://reachable.teachable.com
TERMS OF USE -- LICENSING for ONE USER: As an individual user (meaning one teacher, tutor, instructor, parent, independent learner), YOU will have an individual license to download One-Day Math materials from Teachers Pay Teachers for use only by YOU and the students you teach directly, face to face. Any other individual user should download a separate copy for individual use.
LICENCING for GROUPS: Purchase a multiple license or contact the author to negotiate a group license before you share this resource for a school site, agency, group, or for distance learning where students are not face-to-face with one teacher. See the Resource Licensing Policy: https://www.teacherspayteachers.com/Terms-of-Service