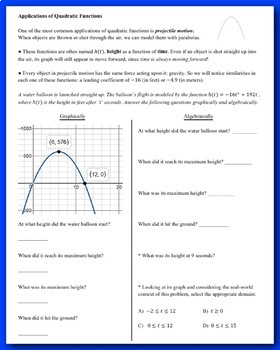
Applications of Quadratic Functions - Modeling Real World Problems Guided Notes

Rated 4.94 out of 5, based on 31 reviews

4.9 (31 ratings)

;

Eddie McCarthy

1.2k Followers

Grade Levels

7th - 12th, Homeschool

Subjects

Algebra, Graphing, Algebra 2

Resource Type

Worksheets, Homework, Scaffolded Notes

Standards

CCSSHSA-SSE.B.3b

CCSSHSA-CED.A.3

CCSSHSA-REI.B.4b

CCSSHSF-IF.B.5

CCSSHSF-IF.C.7

Formats Included

Pages

7 pages

$3.00

Wish List

$3.00

Wish List

Share this resource

Report this resource to TPT

Eddie McCarthy

1.2k Followers

What educators are saying

This was a great tool to use after teaching the features of a quadratic graph and solving quadratic's. It really helped tie the 2 units together and answer their timeless when qwill we ever use this questions.

— Susan C.

Rated 5 out of 5

The problems in the notes and assignment were great for helping my students understand how quadratic functions can be used to model problems.

— Melissa B.

Rated 5 out of 5

Description

Standards

⁵

Reviews

³¹

Q&A

More fromEddie McCarthy

Description

This lesson is part of my Quadratic Functions Unit

This lesson includes 5 pages of guided notes and a 2 page assignment.

Students learn about real-world applications of quadratic functions in the order below. They will:

- Learn what projectile motion is

- Answer questions graphically and algebraically for 3 different projectile motion functions, then practice many more algebraically

- Learn how to answer common questions involving projectile motion (initial height, maximum height, time it took to reach maximum height, time it took to land, etc.)

- Learn what an appropriate domain is when working with real-world problems

- Learn about profit functions and answer similar questions (initial, max, etc.)

- Explore a cost function that opens up

Answer key is included!

Related lessons:

Quadratic Functions: Standard Form

Quadratic Functions: Finding Intercepts

Solving Quadratics by Graphing

Characteristics of Quadratic Functions (Graphic Organizer)

Solving Quadratic Equations (Graphic Organizer)

Related Activity:

Solving Quadratic Equations by Factoring - Word Scramble Activity

Total Pages

7 pages

Answer Key

Included

Teaching Duration

2 days

Last updated Feb 27th, 2017

Report this resource to TPT

Reported resources will be reviewed by our team. Report this resource to let us know if this resource violates TPT’s content guidelines.

Standards

to see state-specific standards (only available in the US).

CCSSHSA-SSE.B.3b

Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines.

CCSSHSA-CED.A.3

Represent constraints by equations or inequalities, and by systems of equations and/or inequalities, and interpret solutions as viable or non-viable options in a modeling context. For example, represent inequalities describing nutritional and cost constraints on combinations of different foods.

CCSSHSA-REI.B.4b

Solve quadratic equations by inspection (e.g., for 𝘹² = 49), taking square roots, completing the square, the quadratic formula and factoring, as appropriate to the initial form of the equation. Recognize when the quadratic formula gives complex solutions and write them as 𝘢 ± 𝘣𝘪 for real numbers 𝘢 and 𝘣.

CCSSHSF-IF.B.5

Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes. For example, if the function 𝘩(𝘯) gives the number of person-hours it takes to assemble 𝘯 engines in a factory, then the positive integers would be an appropriate domain for the function.

CCSSHSF-IF.C.7

Graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases.

Reviews

Questions & Answers

Eddie McCarthy

See all 106 resources

1.2k Followers